1. Математика
Функции — основа математического анализа и других разделов.
Где и как используются:
- Алгебра:
— Линейные функции \( (y = kx + b) \) описывают прямые зависимости
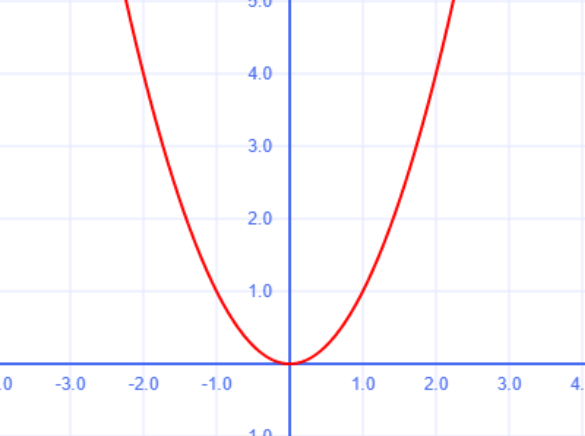
— Квадратичные функции \( (y = ax^2 + bx + c) \) моделируют траектории движения тел - Геометрия:
— Уравнение окружности \( (x^2 + y^2 = r^2) \)
— Параметрические функции для кривых - Оптимизация:
— Поиск экстремумов с помощью производной
2. Программирование
Функции — базовые строительные блоки кода.
Основные задачи:
- Модульность: Разделение кода на логические части
- Рекурсия: Вычисление факториала \( (n! = n \cdot (n-1)!) \)
- Обработка данных: Фильтрация массивов, преобразование форматов
- Функции высшего порядка: Использование map() в Python
Пример на Python:
def calculate_tax(income, rate=0.13):
return income * rate
# Вызов: calculate_tax(100000) → 130003. Физика и инженерия
Применение:
- Механика:
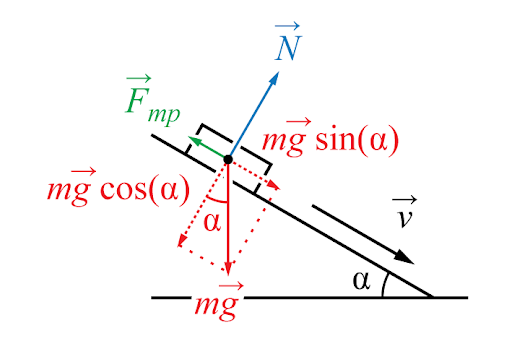
— Движение тела: \( s(t) = v_0 t + \frac{at^2}{2} \)
— Закон Гука: \( F = -kx \) - Электротехника: Закон Ома \( I = \frac{U}{R} \)
- Термодинамика: Уравнение состояния идеального газа \( PV = nRT \)
Пример:
\[ h(t) = h_0 - \frac{gt^2}{2} \]
где \( h(t) \) — высота через время \( t \), \( g \) — ускорение свободного падения.
4. Экономика и финансы
Ключевые модели:
- Спрос и предложение:
— \( Q_d = a - bP \) (спрос)
— \( Q_s = c + dP \) (предложение) - Производственные функции: \( Y = A \cdot K^\alpha L^\beta \)
- Финансовые расчеты: Сложные проценты \( S = P \cdot (1 + \frac{r}{n})^{nt} \)
Пример:
\[ U(x, y) = x^{0.5} \cdot y^{0.5} \]
где \( x \) и \( y \) — количества товаров.
5. Медицина и биология
Области применения:
- Фармакокинетика: Концентрация лекарства \( C(t) = C_0 \cdot e^{-kt} \)
- Рост популяций: Логистическая модель \( P(t) = \frac{K}{1 + (K/P_0 - 1)e^{-rt}} \)
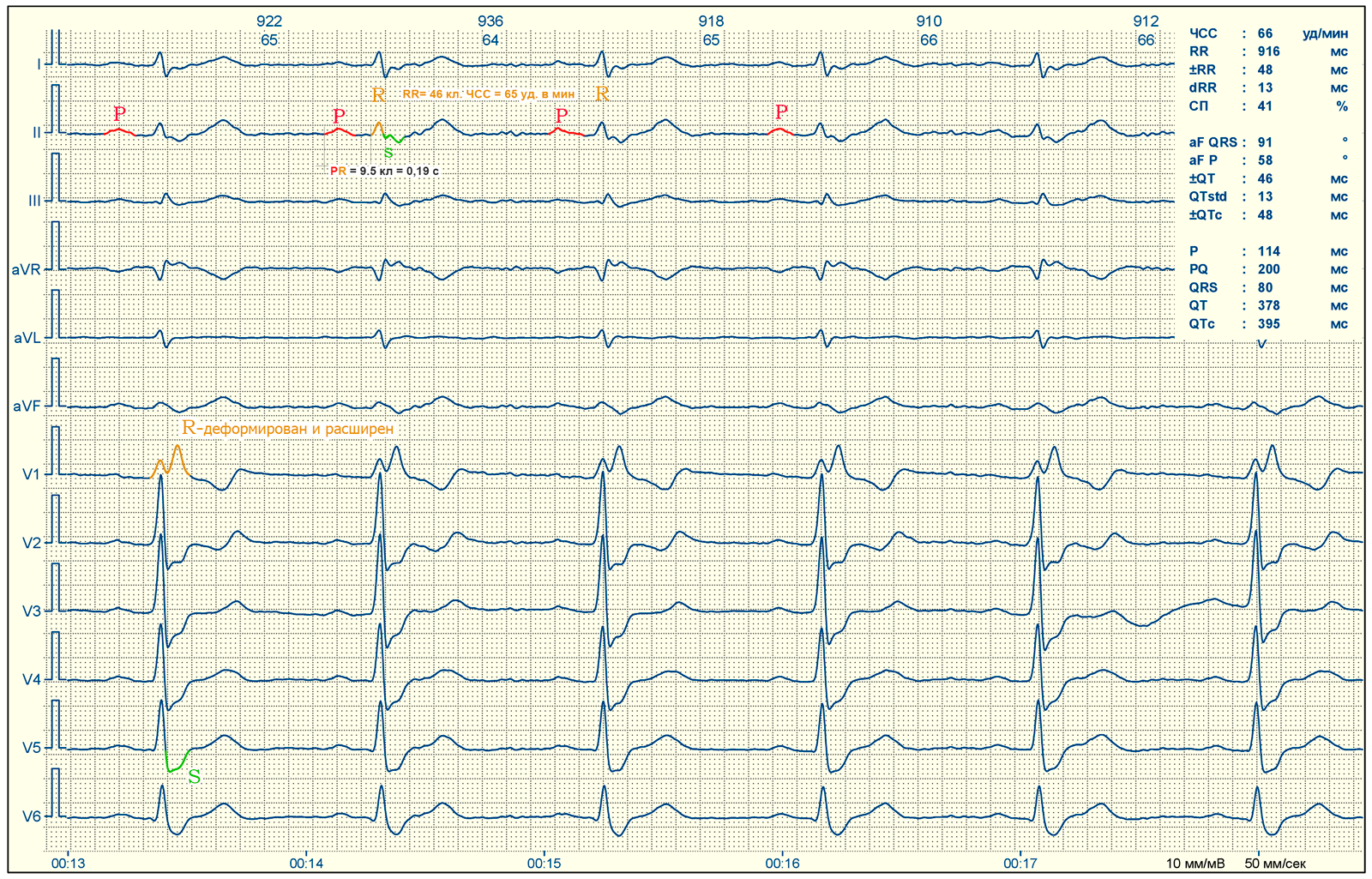
- Диагностика: Анализ ЭКГ с преобразованием Фурье
Модель эпидемии (SIR):
\[
\begin{cases}
\frac{dS}{dt} = -\beta SI, \\
\frac{dI}{dt} = \beta SI - \gamma I, \\
\frac{dR}{dt} = \gamma I,
\end{cases}
\]
6. Искусственный интеллект и машинное обучение
Основные роли:
- Функции активации:
— ReLU: \( f(x) = \max(0, x) \)
— Softmax - Функции потерь: MSE \( L = \frac{1}{n}\sum (y_i - \hat{y}_i)^2 \)
- Оптимизация: Градиентный спуск
Пример:
\[ \hat{y} = w_1 x_1 + w_2 x_2 + b \]
7. Повседневная жизнь
Примеры:
- Кулинария: Пересчет ингредиентов \( \text{ингредиенты} = \text{базовое количество} \times \frac{N}{4} \)
- Путешествия: Расчет времени \( \text{время} = \frac{\text{расстояние}}{\text{скорость}} \)
- Умные устройства: Регулировка температуры термостатом
Пример:
\[ \text{Стоимость} = \frac{\text{расстояние} \times \text{расход топлива}}{100} \times \text{цена за литр} \]
Итог
Функции — универсальный инструмент для:
- Построения предсказуемых моделей
- Оптимизации процессов
- Анализа данных
- Автоматизации рутины
Чем сложнее система, тем больше вложенных функций требуется для её анализа.