Функция квадратного корня: полный разбор
\[ y = \sqrt{x} \]
Она описывает зависимость, где каждому неотрицательному \( x \) соответствует неотрицательное \( y \), такое что \( y^2 = x \).
1. График функции квадратного корня
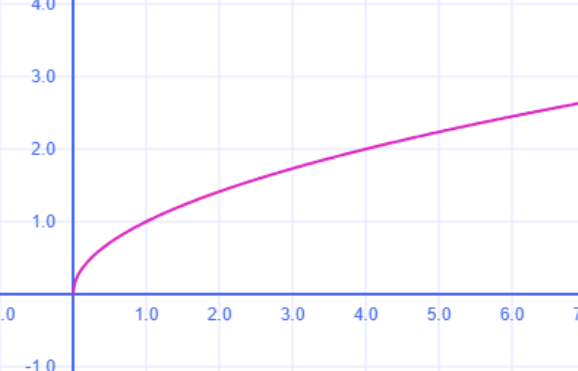
График представляет собой правую ветвь параболы, повёрнутую на 90°:
- Начало координат: \( (0; 0) \).
- Форма: Плавная возрастающая кривая.
- Особенности:
- Не определена для \( x < 0 \).
- Замедление роста при увеличении \( x \).
Пример:
График проходит через точки:
\( (0; 0) \), \( (1; 1) \), \( (4; 2) \), \( (9; 3) \).
2. Область определения и область значений
- Область определения: \( x \geq 0 \).
- Область значений: \( y \geq 0 \).
3. Свойства функции
- Монотонность: Возрастает на всей области определения.
- Выпуклость: Направлена вниз.
- Непрерывность: Непрерывна для \( x \geq 0 \).
4. Построение графика
Алгоритм:
- Отметьте начало координат.
- Используйте точки с идеальными квадратами.
- Соедините плавной кривой.
Пример таблицы для \( y = \sqrt{x} \):
| \( x \) | 0 | 1 | 4 | 9 | 16 |
|---|---|---|---|---|---|
| \( y \) | 0 | 1 | 2 | 3 | 4 |
5. Примеры задач
Задача 1: Область определения
Условие: \( y = \sqrt{2x - 6} \).
\[ 2x - 6 \geq 0 \quad \Rightarrow \quad x \geq 3 \]
Задача 2: Решение уравнения
Условие: \( \sqrt{x} = 5 \).
\[ x = 25 \]
6. Преобразования графика
- Сдвиги:
- \( y = \sqrt{x - a} \) — вправо.
- \( y = \sqrt{x} + b \) — вверх.
- Растяжение/сжатие:
\( y = 3\sqrt{x - 2} + 1 \)