Квадратичная функция

Квадратичная функция: полный разбор для ОГЭ

y = ax² + bx + c, где a ≠ 0

Здесь:

a, b, c — коэффициенты (числа)
x — независимая переменная

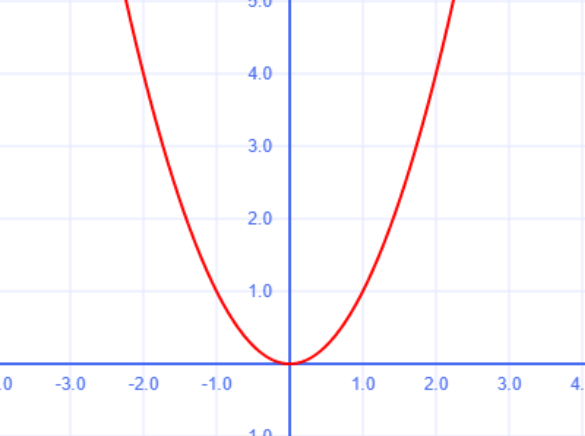
1. График квадратичной функции — парабола

Парабола — это кривая, симметричная относительно вертикальной прямой (оси симметрии). Её форма зависит от коэффициента a:

Если a > 0, ветви параболы направлены вверх
Если a < 0, ветви направлены вниз

Примеры:

y = 2x² → парабола с ветвями вверх

y = -x² + 3 → парабола с ветвями вниз

2. Вершина параболы

Вершина — точка, где парабола меняет направление (минимум или максимум).

x₀ = -b/(2a)
y₀ = ax₀² + bx₀ + c

Пример:

Найти вершину параболы y = x² - 4x + 5

x₀ = -(-4)/(2·1) = 2
y₀ = 2² - 4·2 + 5 = 1
Вершина: (2; 1)

3. Ось симметрии

Это вертикальная прямая, проходящая через вершину:

x = x₀ = -b/(2a)

Пример:

Для y = 3x² - 6x + 1 ось симметрии:

x = 1

4. Точки пересечения с осями

С осью Y:

x = 0 ⇒ y = c ⇒ (0; c)

С осью X (корни функции):

ax² + bx + c = 0

D = b² - 4ac
x₁,₂ = (-b ± √D)/(2a)

Пример:

Найти корни y = x² - 5x + 6

D = (-5)² - 4·1·6 = 1
x₁ = (5 + 1)/2 = 3
x₂ = (5 - 1)/2 = 2
Точки: (3; 0) и (2; 0)

5. Область определения и область значений

Область определения: x ∈ ℝ
Область значений:
• a > 0 ⇒ y ≥ y₀
• a < 0 ⇒ y ≤ y₀

Пример:

Для y = -2x² + 4x - 1:

a = -2 < 0
Вершина: (1; 1)
Область значений: y ≤ 1

6. Свойства квадратичной функции

При a > 0:
• Убывает на (-∞; x₀]
• Возрастает на [x₀; +∞)

При a < 0:
• Возрастает на (-∞; x₀]
• Убывает на [x₀; +∞)

Экстремум:

• a > 0: минимум в вершине (y₀)
• a < 0: максимум в вершине (y₀)

7. Преобразования графика

y = a(x - h)² + k

где (h; k) — вершина

Сдвиги:

y = a(x - h)² + k
→ сдвиг на h вправо и k вверх

Растяжение/сжатие:

|a| > 1 → парабола уже
0 < |a| < 1 → парабола шире

Пример:

y = (x - 3)² + 2 → вершина (3; 2)