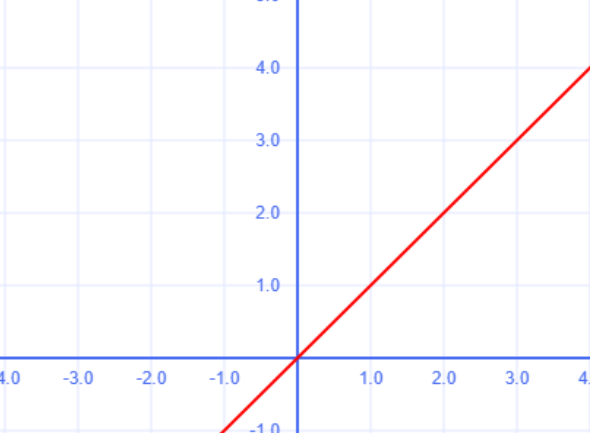
Линейная функция

Линейная функция

Здесь:

• \( k \) — угловой коэффициент (определяет наклон прямой)
• \( b \) — свободный член (точка пересечения с осью \( Y \))
• \( x \) — переменная

1. График линейной функции — прямая

Прямая — это бесконечная линия, которая может быть:

• Возрастающей, если \( k > 0 \)
• Убывающей, если \( k < 0 \)
• Горизонтальной, если \( k = 0 \) (частный случай: \( y = b \))

2. Угловой коэффициент (k)

• Определяет крутизну наклона:
  • Чем больше \( |k| \), тем круче прямая
  • Если \( k = 0 \), прямая параллельна оси \( X \)
• Знак \( k \):
  • \( k > 0 \) → функция возрастает (график идёт вверх направо)
  • \( k < 0 \) → функция убывает (график идёт вниз направо)

3. Точка пересечения с осью Y

Прямая всегда пересекает ось \( Y \) в точке \( (0; b) \).

4. Точка пересечения с осью X

Чтобы найти точку пересечения с осью \( X \), решите уравнение \( kx + b = 0 \):

5. Область определения и область значений

• Область определения: \( x \in \mathbb{R} \) (все действительные числа)
• Область значений:
  • Если \( k \ne 0 \): \( y \in \mathbb{R} \)
  • Если \( k = 0 \): \( y = b \) (единственное значение)

6. Свойства линейной функции

1. Монотонность:
   • Возрастает при \( k > 0 \)
   • Убывает при \( k < 0 \)
   • Постоянна при \( k = 0 \)
2. Скорость изменения:
   \[ k = \frac{\Delta y}{\Delta x} \]
3. Отсутствие экстремумов: Нет максимумов и минимумов

7. Преобразования графика

1. Сдвиги:
   • \( y = kx + b + c \) → сдвиг вверх на \( c \)
   • \( y = k(x - a) + b \) → сдвиг вправо на \( a \)
2. Растяжение/сжатие:
   • \( y = m \cdot (kx + b) \) → растяжение вдоль оси \( Y \)
   • \( y = k(mx) + b \) → сжатие вдоль оси \( X \)
3. Отражения:
   • \( y = -kx + b \) → отражение относительно оси \( X \)
   • \( y = k(-x) + b \) → отражение относительно оси \( Y \)