Гипербола: полный разбор
\[ y = \frac{k}{x}, \quad k \ne 0 \]
Она описывает зависимость, при которой увеличение одной величины приводит к уменьшению другой, и наоборот.
1. График гиперболы
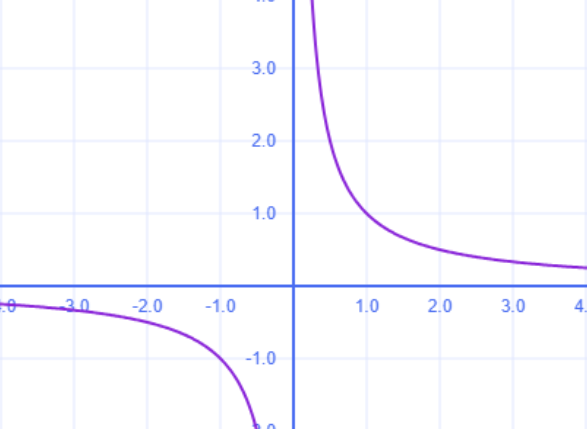
График состоит из двух симметричных ветвей:
- При \( k > 0 \): Ветви в I и III четвертях.
- При \( k < 0 \): Ветви во II и IV четвертях.
- Асимптоты: \( x = 0 \), \( y = 0 \).
Примеры:
\( y = \frac{4}{x} \) (k > 0), \( y = -\frac{2}{x} \) (k < 0)
2. Область определения и область значений
- Область определения: \( x \in \mathbb{R}, x \ne 0 \).
- Область значений: \( y \in \mathbb{R}, y \ne 0 \).
3. Свойства гиперболы
- Нечётность:
\[ f(-x) = -f(x) \]
- Монотонность:
- Убывает при \( k > 0 \).
- Возрастает при \( k < 0 \).
4. Построение графика
Алгоритм:
- Определите знак \( k \).
- Постройте таблицу значений.
- Нарисуйте ветви, приближающиеся к асимптотам.
Пример таблицы для \( y = \frac{6}{x} \):
| \( x \) | -6 | -3 | -2 | 2 | 3 | 6 |
|---|---|---|---|---|---|---|
| \( y \) | -1 | -2 | -3 | 3 | 2 | 1 |
5. Примеры задач
Задача 1: Найти коэффициент \( k \)
Условие: Гипербола проходит через точку \( (4; -5) \).
\[ k = -20 \]
Задача 2: Пересечение с прямой
Условие: \( y = \frac{8}{x} \) и \( y = 2x \).
Точки пересечения: \( (2; 4) \), \( (-2; -4) \).
6. Преобразования графика
\[ y = \frac{k}{x - a} + b \]
- Сдвиг вправо на \( a \), вверх на \( b \).
- Новые асимптоты: \( x = a \), \( y = b \).
Пример:
\( y = \frac{-4}{x - 3} + 2 \)
Асимптоты: \( x = 3 \), \( y = 2 \).