Показательная функция: полный разбор
\[ y = a^x, \quad a > 0, \, a \ne 1 \]
Она описывает экспоненциальный рост (при \( a > 1 \)) или убывание (при \( 0 < a < 1 \)) и применяется в биологии, экономике, физике.
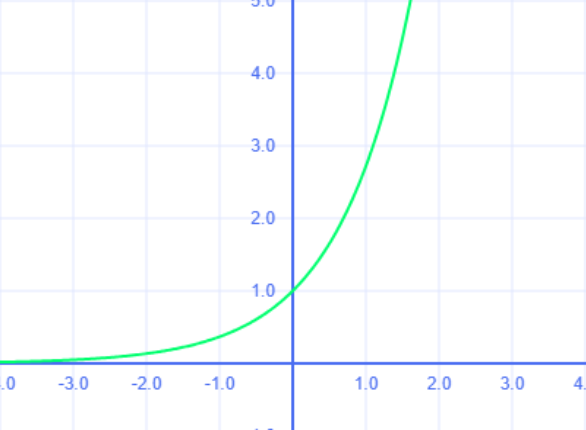
1. График показательной функции
График имеет форму плавной кривой:
- При \( a > 1 \):
- Возрастает, стремясь к \( +\infty \) при \( x \to +\infty \).
- Приближается к оси \( X \) (\( y = 0 \)) при \( x \to -\infty \).
- При \( 0 < a < 1 \):
- Убывает, стремясь к \( 0 \) при \( x \to +\infty \).
- Приближается к \( +\infty \) при \( x \to -\infty \).
- Общие черты:
- Проходит через точку \( (0; 1) \).
- Горизонтальная асимптота \( y = 0 \).
2. Область определения и область значений
- Область определения: \( x \in \mathbb{R} \).
- Область значений: \( y > 0 \).
3. Свойства показательной функции
- Монотонность:
- Возрастает при \( a > 1 \).
- Убывает при \( 0 < a < 1 \).
- Экспонента (\( a = e \)):
\[ y = e^x \]
- Производная:
\[ \frac{d}{dx} a^x = a^x \ln a \]
4. Построение графика
Алгоритм:
- Отметьте точку \( (0; 1) \).
- Для \( a > 1 \) добавьте точки \( (1; a) \), \( (-1; 1/a) \).
- Соедините плавной кривой с асимптотой \( y = 0 \).
Пример таблицы для \( y = 2^x \):
| \( x \) | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| \( y \) | 0.25 | 0.5 | 1 | 2 | 4 |
5. Примеры задач
Задача 1: Решение уравнения
Условие: \( 3^{x+2} = 81 \).
\[ x = 2 \]
Задача 2: Нахождение основания
Условие: Функция проходит через \( (2; 25) \).
\[ a = 5 \]
6. Преобразования графика
- Сдвиги:
\[ y = 2^{x - 3} + 1 \]
- Отражения:
\[ y = -e^x \, \text{или} \, y = e^{-x} \]