Кубическая функция: полный разбор
\[ y = ax^3 + bx^2 + cx + d, \quad a \ne 0 \]
Она описывает нелинейные зависимости и часто встречается в физике, экономике и инженерии.
1. График кубической функции
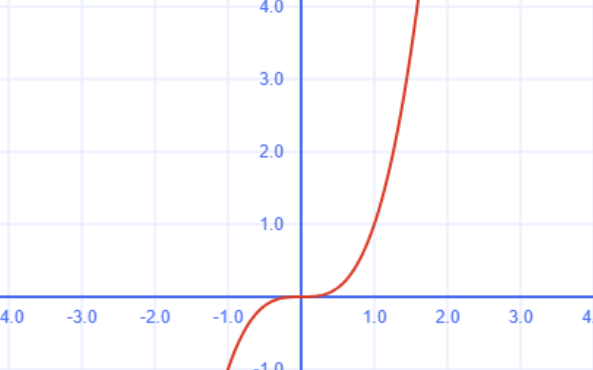
График называется кубической параболой:
- Поведение на бесконечности:
- При \( a > 0 \): \( y \to +\infty \) при \( x \to +\infty \), \( y \to -\infty \) при \( x \to -\infty \).
- При \( a < 0 \): \( y \to -\infty \) при \( x \to +\infty \), \( y \to +\infty \) при \( x \to -\infty \).
- Особые точки: Экстремумы и точка перегиба.
Примеры:
\( y = x^3 \) — классическая кубическая парабола
\( y = x^3 - 3x \) — с экстремумами и точкой перегиба
2. Область определения и область значений
- Область определения: \( x \in \mathbb{R} \).
- Область значений: \( y \in \mathbb{R} \).
3. Свойства кубической функции
- Непрерывность: Непрерывна на всей числовой прямой.
- Количество корней: 1, 2 или 3 действительных корня.
- Экстремумы: Находятся через первую производную.
\[ y' = 3ax^2 + 2bx + c \]
4. Построение графика
Алгоритм:
- Найдите корни уравнения.
- Вычислите экстремумы и точку перегиба.
- Постройте таблицу значений.
Пример таблицы для \( y = x^3 - 3x \):
| \( x \) | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| \( y \) | -2 | 2 | 0 | -2 | 2 |
5. Примеры задач
Задача 1: Найти корни уравнения
Условие: \( x^3 - 6x^2 + 11x - 6 = 0 \).
\[ (x - 1)(x - 2)(x - 3) = 0 \quad \Rightarrow \quad x = 1; 2; 3 \]
Задача 2: Определить экстремумы
Условие: \( y = x^3 - 3x^2 - 9x + 5 \).
Максимум \( (-1; 10) \),
Минимум \( (3; -22) \).
Минимум \( (3; -22) \).
6. Преобразования графика
- Сдвиги:
\[ y = 2(x - 1)^3 + 4 \]
- Отражения:
\[ y = -ax^3 \]