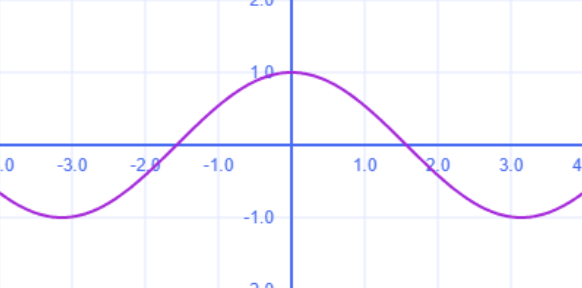
Косинусоида: полный разбор
\[ y = \cos(x) \]
Она описывает периодические колебания, аналогичные синусоиде, но смещённые по фазе. Широко используется в физике, инженерии и технике.
1. График косинусоиды
График имеет вид волнообразной кривой с ключевыми особенностями:
- Периодичность: Повторяется каждые \( 2\pi \).
- Амплитуда: Максимальное отклонение от оси \( X \) равно 1.
- Фаза: Начальная точка при \( x = 0 \): \( (0; 1) \).
- Точки пересечения с осями:
- С осью \( X \): \( x = \frac{\pi}{2} + \pi n \), \( n \in \mathbb{Z} \).
- С осью \( Y \): \( (0; 1) \).
Пример:
\( y = \cos(x) \) — классическая косинусоида с амплитудой 1 и периодом \( 2\pi \).
2. Область определения и область значений
- Область определения: \( x \in \mathbb{R} \).
- Область значений: \( y \in [-1; 1] \).
3. Свойства косинусоиды
- Периодичность:
\[ \cos(x + 2\pi) = \cos(x) \]
- Чётность:
\[ \cos(-x) = \cos(x) \]
- Нули функции:
\[ \cos(x) = 0 \quad \Rightarrow \quad x = \frac{\pi}{2} + \pi n \]
- Экстремумы:
- Максимум: \( \cos(2\pi n) = 1 \).
- Минимум: \( \cos(\pi + 2\pi n) = -1 \).
4. Построение графика
Алгоритм:
- Отметьте ключевые точки на отрезке \( [0; 2\pi] \).
- Продолжите график с учётом периодичности.
Пример таблицы для \( y = \cos(x) \):
| \( x \) | 0 | \( \frac{\pi}{2} \) | \( \pi \) | \( \frac{3\pi}{2} \) | \( 2\pi \) |
|---|---|---|---|---|---|
| \( \cos(x) \) | 1 | 0 | -1 | 0 | 1 |
5. Примеры задач
Задача 1: Найти период функции
Задача: Какой период у \( y = \cos(4x) \)?
\( T = \frac{\pi}{2} \)
Задача 2: Решить уравнение
Задача: Решите \( \cos(x) = \frac{1}{2} \).
\( x = \pm \frac{\pi}{3} + 2\pi n \)
6. Преобразования косинусоиды
\[ y = A \cdot \cos(Bx + C) + D \]
- \( A \) — амплитуда.
- \( B \) — период \( T = \frac{2\pi}{|B|} \).
- \( C \) — горизонтальный сдвиг.
Примеры преобразований:
\( y = 2\cos\left(x - \frac{\pi}{2}\right) \) — сдвиг вправо.
\( y = \cos(2x) + 1 \) — период \( \pi \).